Dans l'[épisode précédent](/articles/On%20va%20à%20la%20pêche.html), nous avons vu que tester chaque case de la «rivière aux Barpaus» une fois seulement avant d'aller pêcher sur la suivante augmentait les probabilités de rencontrer un Barpau pour un nombre de pêche donné, et donc que, statistiquement, cette stratégie de pêche diminuait le nombre de pêches à tenter avant de trouver une «case à Barpau» (pour reprendre les notations de l'article précédent, `C⁺`, sérieusement allez le lire si vous ne l'avez pas déjà lu, sinon celui-ci n'a aucun intérêt).
La méthode que nous avions suivie reposait sur une hypothèse, tout à fait fondée initialement mais de plus en plus discutable et même carrément fausse au-delà de 394 cases testées dans la rivière, qui consistait à considérer une distribution uniforme de probabilité pour les cases `C⁺` (c.f. le début du § «Stratégie, stratégie»). Mais comme nous l'avions vu, les tirages ne sont pas indépendants et `P⁺` évolue au fil du résultat de nos tirages, puisque par exemple si nous observons 6 cases distinctes avec des Barpaus, alors il n'est pas besoin de poursuivre l'expérience : la probabilité que les autres cases contiennent des Barpaus sachant cela est nulle (sauf blague de l'équipe de développement du jeu, mais si l'on accepte la prémice «il n'y a que 6 cases contenant des Barpaus dans cette rivière» alors elle est bien nulle). Et si on regardait un peu plus en détail comment cette fonction de probabilité évolue au fil des tirages et de leurs résultats ?
## Une méthode
Et pour cela, quoi de mieux que revenir aux bases comme nous l'avons fait avec nos cases ? Cette probabilité, après tout, ne représente que le ratio du nombre de cas vérifiant une propriété qui nous intéresse sur le nombre de cas total. Nous allons donc faire pas mal de dénombrement. Pour se chauffer, commençons par évaluer la taille totale de l'ensemble dans lequel nous travaillons : l'espace de tous les tirages de rivière à Barpau possibles.
Notre rivière fait 400 cases, parmi lesquelles se trouvent 6 cases `C⁺` et 394 cases `C⁻`. Les cases à Barpau et les cases sans sont absolument indiscernables entre elles. Un tirage de rivière dépend donc seulement de la «position» des 6 cases `C⁺` dans l'ensemble des 400 cases totales. La première case `C⁺` peut être choisie parmi les 400 cases libres initialement «vides» de la rivière : il y a 400 choix possibles à cette étape. La deuxième doit être choisie dans une des cases restantes, soit 399 choix, et ainsi de suite, le nombre de case possible diminuant d'une unité à chaque fois.
<pre class="example">
N<sub>choix</sub> = 400 × 399 × 398 × … × 395 = 400! / 394!
</pre>
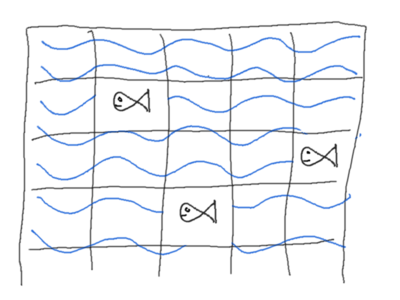
À un détail près : nos cases sont indiscernables, donc leur ordre n'a aucune importance puisqu'il n'a aucune influence pour nous. Nous avons trouvé 400 choix pour la «première», mais il ne s'agit que de l'ordre du choix, rien ne nous garantit que la case choisie sera la «première» dans l'ordre arbitraire avec lequel nous considèrerions la rivière. Peut-être qu'il s'agira de la 11ème case, disons, mais rien n'empêche alors que le choix de la «deuxième» (toujours en terme d'ordre de tirage) case `C⁺` soit la 3ème case (dans un ordre arbitraire quelconque de parcours de la rivière fixé préalablement — celui dans lequel on va fouiller la rivière par exemple). Si nous n'autorisions que des cases d'indice plus grands que la première, il n'y aurait plus 399 choix possibles pour la deuxième mais un nombre qui dépendrait de l'indice de la première (qui d'ailleurs n'aurait plus que 395 valeurs possibles et pas 400, puisque les 5 autres devraient être placées «après»), ce qui compliquerait dramatiquement les calculs. Nous, notre méthode est bien plus simple, il suffit juste de garder à l'esprit que dans notre dénombrement en cours nous avons plusieurs tirages identiques pour ce qui nous concerne : par exemple `[11, 3, …]` et `[3, 11, …]` (dans l'exemple précédent, la «première» aurait aussi pu être la 3ème case et la «deuxième» la 11ème).
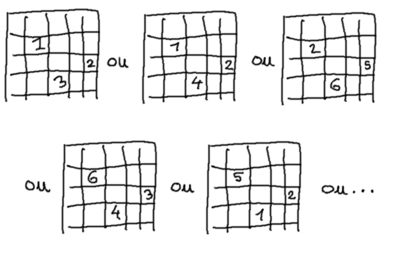
Bon, mais rien auquel il ne soit facile de remédier, étant donné un tirage unique de cases, on sait qu'il aura donné naissance dans l'analyse précédente à autant de tirages identiques qu'il est possible de permuter 6 éléments : 6 places pour le premier, 5 pour le deuxième, etc.
<pre class="example">
N<sub>permutations</sub> = 6 × 5 × 4 × … × 1 = 6!
</pre>
Le nombre total de tirages de rivière que nous cherchons est donc en fait
<pre class="example">
N<sub>rivières</sub> = 400! / (6! × 394!)
</pre>
Oh tiens ! On retombe pile sur une formule de coefficient binomial. Ce nombre, on le note aussi couramment `C(400, 6)`. Si comme moi vous passez votre temps à vous perdre entre les [k-combinaisons](https://fr.wikipedia.org/wiki/Combinaison_%28math%C3%A9matiques%29) et les [k-arrangements](https://fr.wikipedia.org/wiki/Arrangement) parce qu'on vous présente ça comme «des machins tout faits» au contenu desquels il faut surtout pas réfléchir, vous l'avez, là, votre illustration : ce qu'on a commencé à calculer, avant de diviser par le nombre de permutations, c'est le nombre de k-arrangements, le nombre de façons de choisir k éléments **discernables** parmi N éléments; une fois réduit en divisant par le nombre de permutations qu'on peut faire entre ces k éléments, il ne reste plus que le nombre de k-combinaisons, c'est à dire le nombre de façons de choisir k éléments **indiscernables**. Voilà, maintenant vous ne confondrez plus jamais les deux.
Propriété sympa (et rassurante !) du nombre de combinaisons `C(N, k)` : il est symétrique, c'est à dire que
<pre class="example">
(1) C(N, k) = C(N, N-k)
</pre>
Et heureusement !! En effet, au début de notre raisonnement nous avons commencé par placer les 6 cases `C⁺` parce que ça paraissait clairement plus commode vu qu'il y en avait moins, mais pourquoi n'aurions-nous pas pu faire exactement le même raisonnement en plaçant nos 394 cases `C⁻` plutôt ? Juste pour embêter le monde, hein ? Et bin voilà, on sait qu'on aurait obtenu `C(400, 394)`, et comme nous avons le bonheur de reconnaître un objet classique et parfaitement connu des mathématiques, on sait que `C(400, 394) = C(400, 6)`, et donc qu'on aurait obtenu exactement le même nombre de rivières possibles. Ouf. Mine de rien, c'est important la cohérence. Peut-être qu'on peut se servir de cet remarque pour retenir, à l'inverse, cette propriété des nombre de combinaisons ? «Hmmmm pourquoi c'est symétrique, déjà ? — parce que c'est le nombre de choix de k parmi N, et qu'en choisir k, c'est exactement équivalent à en choisir N-k et à pas les prendre !»
## Un bourgeon
Nous avons fait le plus dur. Ce raisonnement que nous avons redétaillé va nous resservir encore et encore. Il ya donc `C(400, 6)` rivière possible. Ça fait combien au fait ? (oui, apparemment les gens veulent voir des applications numériques, alors pourquoi pas hein ?)
<pre class="example">
N<sub>rivières</sub> = C(400, 6) = 5.4785578386e12
</pre>
De l'ordre de 5000 milliards de rivières possibles. C'est dingue comme on se retrouve vite à manipuler des gros nombres dès qu'il y a des histoires de combinaisons impliquées.
Bon, et alors, des rivières telle que la première case soit une case à Barpau, combien y en a-t'il ? Faisons exactement le même raisonnement. Parmi toutes les rivières possibles, celles dont la première case est une case `C⁺` sont déterminées par… le fait que la première case est `C⁺`, donc, pas de choix sur cette première case, juste une contrainte mais ensuite, plus rien. Il existe autant de rivières comme ça qu'on a pu distribuer les 5 cases `C⁺` restantes sur les 399 cases de rivière encore indéterminées. Bin voilà, même raisonnement que ci-dessus, et on arrive directement à la conclusion que
<pre class="example">
N<sub>rivières|C⁺(1)</sub> = C(399, 5) = 8.2178367579e10
</pre>
Ah, tiens, et ça nous fait combien de chances, ça, que cette première case soit `C⁺` ? Et bien
<pre class="example">
C(399, 5) / C(400, 6) = (399! / (5! × 394!)) / (400! / (6! × 394!))
= (399! × 6! × 394!) / (5! × 394! × 400!)
= 6 / 400
</pre>
Six divisé par quatre-cent !! Oui, il y a 6 cases à répartir sur 400 cases, la première case, qui n'est encore pas du tout influencée par la distribution des autres cases, a exactement la probabilité de la distribution uniforme que nous avions choisie. En restant aux applications numériques pour estimer cette probabilité, nous n'aurions peut-être pas reconnu dans le 1.5% obtenu la probabilité simplifiée de l'article précédent. Bon, c'est rassurant, tout ne doit pas être complètement faux pour qu'on obtienne quelque chose d'aussi cohérent. Tiens, et si on s'intéressait maintenant à l'autre issue pour la première case, qu'elle soit `C⁻` ? Oui, c'est évident, numériquement la probabilité en est de 98.5%, soit `394/400`[^P⁺P⁻], mais reprenons le raisonnement qui nous a si bien servi jusqu'ici.
Pour «générer» une rivière dont la première case est `C⁻`, il faut imposer donc ce premier paramètre et ensuite il nous reste 6 cases à placer dans le reste de la rivière, soit 399 cases, soit `C(399, 6)` rivières possibles. Bien sûr, on pourrait reproduire le calcul ci-dessus avec des simplifications dans les factorielles pour exhiber une probabilité de `394/400` (faites-le, ça fait du bien l'exercice, moi mes brouillons en sont déjà couverts alors je m'en dispense). Mais surtout, on sait que les deux cas `C⁺` et `C⁻` pour cette première case sont mutuellement exclusifs et sont les seuls possibles. On a donc :
<pre class="example">
C(399, 6) + C(399, 5) = C(400, 6)
</pre>
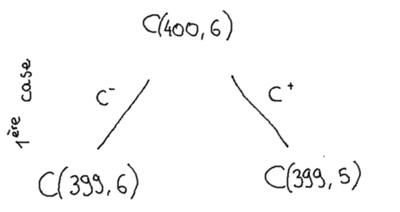
Encore une égalité écrite dans cette article qui ne va certainement pas révolutionner les mathématiques, et pour cause, cette égalité est une propriété bien connue des coefficients binomiaux et en fait vérifiée pour tout `k` et `N` :
<pre class="example">
(2) C(N-1, k) + C(N-1, k-1) = C(N, k)
</pre>
Rien de révolutionnaire, donc, mais ce qui m'intéresse ici, c'est qu'en «redécouvrant» tout ça, nous nous sommes donnés une compréhension solide et une représentation concrète de ce qui est à l'œuvre dans cette formule plus générale. En fait, ce que dit cette formule, c'est que pour choisir `k` éléments parmi `N`, il suffit de prendre le premier et d'en choisir `k-1` parmi les `N-1` restant, ou d'ignorer le premier et de finalement choisir tous les `k` parmi les `N-1` restant. Là, cette formule a du sens, et nous allons l'appliquer généreusement.
## Et bien grimpons maintenant
Car ce que nous avons fait sur «l'état initial» comprenant toutes les rivières possibles pour obtenir de l'information sur la première case, nous pouvons le faire ensuite sur chaque issue possible pour obtenir de l'information sur la deuxième case.
À chaque état possible pour une case, deux états possibles pour la case suivante : ou bien la case suivante est une case à Barpau (cas «`k-1`» dans la formule `(2)`), ou bien elle ne l'est pas (cas «`k`»). Et tous les chemins possibles depuis la racine représentent toutes les possibilité que telle ou telle case ait été `C⁺` ou `C⁻`.
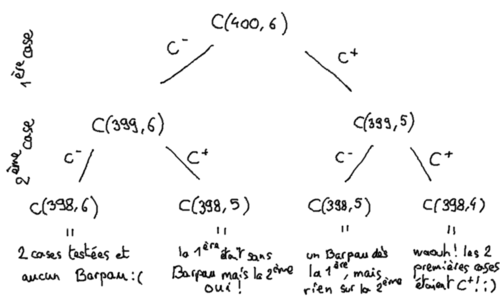
Nous allons même pouvoir recommencer à fournir des estimations des probabilités comme nous le faisions dans l'article précédent, car derrière ces nombres absolus de tirages de rivière telle qu'une case donnée soit ou non `C⁺`, se cache bien évidemment la probabilité du même événement : il suffit de rapporter ce nombre à notre nombre total de rivière par lequel nous avons débuté cette analyse, `C(400, 6)`. C'est à dire que maintenant que nous avons bien manipulé nos `C(N, k)` et esquissé des arbres pour voir comment tout s'articulait, on va en fait considérer la quantité équivalente :
<pre class="example">
F(N, k) = C(N, k) / C(400, 6)
</pre>
C'est à dire la fréquence de `k` parmi `N` dans notre univers de rivières possibles. C'est exactement la même chose qu'avant, à un facteur `C(400, 6)` près. En particulier `(2)` reste valable sur les `F` comme elle l'était sur les `C` :
<pre class="example">
(2') F(N-1, k) + F(N-1, k-1) = F(N, k)
</pre>
Supposons que nous pêchions `n` fois sur la première case. Quel est le risque que nous n'ayons pas rencontré de Barpau ? Aller, *once again* tou·tes en cœur : la probabilité que que la case ait été `C⁻` plus celle qu'elle ait été fois `C⁺` et que l'événement contraire «ne pas pêcher un Barpau» se soit produit `n` fois.
<pre>
R(n) = F(399,6) + F(399,5) × 0.85<sup>n</sup>
</pre>
Donc la probabilité que nous ayons rencontré au moins un Barpau en `n` pêches sur la première case est de :
<pre>
P<sub>b</sub>(n) = 1 - (F(399,6) + F(399,5) × 0.85<sup>n</sup>)
</pre>
Rien de bien folichon, pour l'instant on a juste réécrit la formule de l'article précédent en remplaçant les notation `P⁺` et `P⁻` par des expressions issues de notre étude combinatoire. On va rester pêcher `p` fois sur cette première case, donc la formule précédente est valable tant que `n ≤ p`. Ensuite, il suffit de refaire la même analyse que précédement en regardant cette fois la deuxième ligne de notre arbre pour couvrir tous les `n ≤ 2p`:
<pre>
∀ n ≤ 2p, P<sub>b</sub>(p, n) = 1 - (F(398,6) + F(398,5)×0.85<sup>n[p]</sup> + F(398,5)×0.85<sup>p</sup> + F(398,4)×0.85<sup>n</sup>)
</pre>
Elle paraît moche de premier abord, mais en la regardant on voit qu'elle a plein de belles propriétés.
Commençons par regarder les termes dûs au `C⁺`, les termes «actifs», c'est à dire ceux qui dépendent véritablement de `n`, ceux qui traitent les cas «la deuxième case était une case à Barpau» c'est à dire dans l'arbre précédent les deuxième et quatrième issues en regardant depuis la gauche.
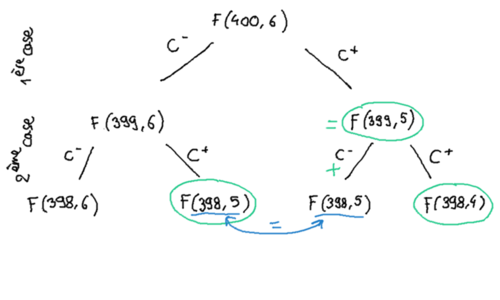
Il y a un terme `F(398, 5)` (`C⁻` puis `C⁺`) et un terme `F(398, 4)` (deux `C⁺`). La somme de ces deux termes est égale, d'après la formule `(2')`, à `F(399, 5)`, qui était la probabilité que la première case soit une case à Barpau. Intuitivement, on voit que ça va se généraliser au fur et à mesure qu'on avance dans les cases, parce que chaque terme `F(n, k)` va donner lieu à un terme `F(n-1, k)` pour une case suivante `C⁻` et `F(n-1, k-1)` pour une suivante `C⁺`. Le terme correspondant à `C⁻`, couvrant un des cas où la case suivante n'est pas case à Barpau sera bien entendu écarté, mais compensé par le terme immédiatement à sa gauche dans l'arbre issu du `C⁺` suivant le nœud adelphe du nœud parent (en gros, on re-synthétise le `F(n-1, k)` manquant comme un `F(n-1, k+1-1)` correspondant à l'enfant `C⁺` du nœud adelphe `F(n-1, k+1)` de `F(n-1, k)` — en terme de chemin depuis la racine de l'arbre, on intervertit seulement les deux étiquettes finales `C⁺ · C⁻` ↔ `C⁻ · C⁺`).
Donc on voit assez facilement en répétant ce résultat à chaque étage, que tous les termes de la somme d'un étage donné se retrouvent à l'étage suivant, décomposés, mais la somme reste donc constante, et en remontant tout ce sous-arbre des «chemins se terminant par un `C⁺`» on retrouve toujours `F(399, 5)`. Ce qui est remarquable, c'est que ce résultat persiste sur les bords, là on pourrait s'attendre à ce qu'il soit menacé (il repose, après-tout, sur la division de chaque nœud de l'arbre en deux nœuds, ce qui n'a plus lieu quand toutes les cases `C⁺` on déjà été trouvées, tout à droite de l'arbre, et quand trop peu ont été trouvées et que les cases suivantes sont forcément `C⁺`, tout à gauche de l'arbre), comme on le verra en détail un peu plus loin.
Par conséquent, si l'interdépendance des états des cases influe sur l'évolution de la probabilité de trouver un Barpau au bout d'un nombre de cases données, en revanche chaque case, individuellement, demeure inaffectée, avec la même probabilité de `F(399, 5) = 6 / 400` d'être `C⁺`. C'est beau quand même. Nous allons conserver cette distinction entre termes «actifs» correspondant à une case en cours `C⁺` et autres termes pour réécrire `Pb(p, n)`
<pre>
∀ n ≤ 2p, P<sub>b</sub>(p, n) = 1 - ([F(398,6) + F(398,5)×0.85<sup>p</sup>] + [F(398,5) + F(398,4)×0.85<sup>p</sup>]×0.85<sup>n[p]</sup>)
</pre>
Puis, en appliquant la même logique que ci-dessus, on va voir chaque terme `F(n, k)` se «diviser» en un `F(n-1, k)` correspondant à une `C⁻` qui contribuera au bloc entre `[…]` «constant» (ne dépendant pas de `n`) à gauche dans la formule ci-dessus et un autre `F(n-1, k-1)` correspondant à une `C⁺` qui contribuera lui au bloc «actif» à droite. Aller, je fais le troisième étage quand même :
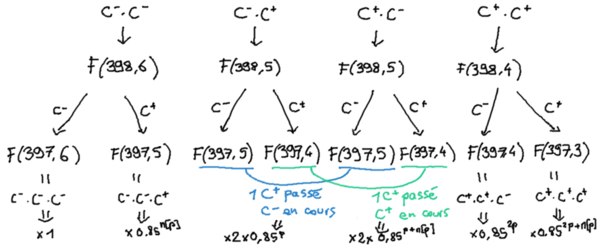
D'où l'on arrive à étendre la formule précédente jusqu'à `n ≤ 3p`:
<pre>
∀ n ≤ 3p, P<sub>b</sub>(p, n) = 1 - ([F(397,6) + 2×F(397,5)×0.85<sup>p</sup> + F(397,4)×0.85<sup>2p</sup>] + [F(397,5) + 2×F(397,4)×0.85<sup>p</sup> + F(397,3)×0.85<sup>2p</sup>]×0.85<sup>n[p]</sup>)
</pre>
Les '2' qui apparaissent sont en fait des coefficients binomiaux ! C'est ça qui est beau, voir naturellement des coefficients binomiaux réapparaître comme facteur de nos termes `F(n, k)`, qui sont eux-même issus de termes binomiaux; ça vient du fait que nos coefficients s'inscrivent dans notre arbre triangulaire, et se retrouvent définis comme somme de deux autres de la ligne précédente exactement comme dans le triangle de [Pascal](https://fr.wikipedia.org/wiki/Triangle_de_Pascal).
```
1
11
121
1331
…
```
À la ligne suivante, les `2×F(397,5)` vont donner `2×F(396,5)` côté `C⁻` qui, combinés avec le `F(396,5)` obtenu du `F(397,5)` du terme «actif», vont bien faire `3×F(396,5)`; pareillement le `F(397,4)` du bloc «constant en `n`» à gauche va, après abaissement de `n` en 396 côté `C⁻` et addition avec les enfants `C⁻` du terme «actif» `2×F(397,4)` donner lieu à `3×F(396,4)×0.85^2p`. La même chose a lieu à droite dans le bloc «actif» en considérant les enfants `C⁺` de chacun des termes de la formule précédente.
Par récurrence, on arrivera à généraliser ce qui précède en
<pre>
(3) Pour n = q×p+r, P<sub>b</sub>(p, n) = 1 - ([Σ(k=0 → min(q, 6)) C(q, k)×F(399-q, 6-k)×0.85<sup>p×k</sup>] + [Σ(k=0 → min(q, 5)) C(q, k)×F(399-q, 5-k)×0.85<sup>p×k</sup>]×0.85<sup>r</sup>)
</pre>
Ça peut paraître un peu tombé du ciel là comme ça mais franchement faites-le, vous allez voir c'est grisant de voir tout bien tomber. Reprenez la dernière ligne ci-dessus, ajoutez-en encore une ou deux et vous verrez très bien ce qui se passe et comment les coefficients se somment par puissances égales de `0.85`.
## Attention à ne pas tomber !
Bon, ça prend tournure cette affaire. Reste à voir ce qui se passe pour de vrai sur les «bords» dont nous parlions plus haut. Comme nous l'avons dit il y a un moment où ça arrête de se diviser; parce qu'il n'y a plus de cases `C⁺` à trouver, sur la droite de l'arbre dès la 6ème ligne, et en bas tout à gauche, à partir de la 394ème ligne parce qu'il reste trop de `C⁺` à «écouler».
Plaçons-nous donc un moment à la 6ème ligne de l'arbre, juste avant d'envisager la possibilité d'épuiser immédiatement les 6 cases pour l'unique (!) distribution de rivière : «les 6 premières cases `C⁺`, toute la suite `C⁻`». Pour ne pas étouffer sur un arbre trop épais (à cet étage, il a déjà 32 nœuds…), cantonnons-nous au sous-arbre issu du préfixe `C⁺·C⁺·C⁺·C⁺` (c'est à dire que nous ne considérons que les tirages de rivières pour lesquelles les 4 premières cases sont `C⁺`).
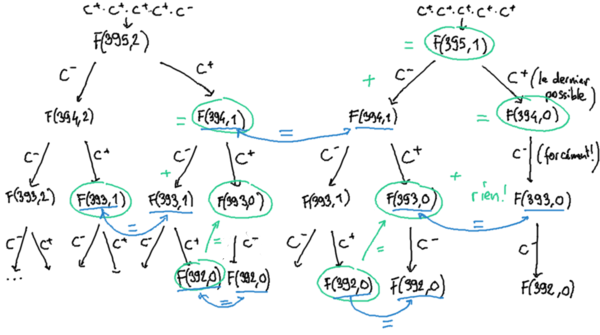
On observe bien ici cette division à chaque étage avec la conservation de la probabilité totale de `F(399, 5)` que la case soit `C⁺` pour l'étage considéré. Le nœud `C⁺·C⁺·C⁺·C⁺·C⁺` considéré, dont la probabilité est `F(395, 1)` s'associerait avec le nœud, non-représenté, immédiatement à la gauche du `F(395, 2)` de la première ligne de ce schéma, valant lui aussi `F(395, 2)` pour «expliquer» le `F(396, 2)` de la ligne immédiatement au-dessus de la portion visible et ainsi de suite, perpétuant de ligne en ligne cette somme totale par ligne des issues «case `C⁺`» égale à `F(399, 5)`. Dans la portion de l'arbre couverte par notre schéma, le `F(395, 1)` de l'ensemble des rivières `C⁺·C⁺·C⁺·C⁺·C⁺·…` se décompose bien en le `F(394, 1)` enfant `C⁺` de l'adelphe `C⁺·C⁺·C⁺·C⁺·C⁻` plus le `F(394, 0)` de son propre enfant `C⁺` qui met le terme à une série de 6 `C⁺` dès les 6 premières cases de la rivière.
Mais passons à la ligne suivante où il se passe quelque chose de particulier : à gauche, rien à signaler, `F(394, 1)` se décompose, comme `F(395, 1)` vient de le faire, en `F(393, 1) + F(393, 0)`, en suivant toujours le même schéma. Mais à droite ! `F(394, 0)` ne peut plus se diviser, et pour cause ! Toutes les 6 cases `C⁺` possibles ont déjà été attribuées, toutes les cases suivantes ne peuvent plus être que `C⁻`, c'est une certitude. Si on reprend un point de vue combinatoire, alors tout le reste est fixé, il n'y a plus de degré de liberté, ce qui ne peut engendrer qu'autant de rivières qu'on en a déjà : `F(393, 0) = F(394, 0)`. Et oui, cette égalité est vérifiée, les deux étant mêmes égaux à `1/C(400, 6)` : nous parlons d'un unique tirage possible de rivière, déterminé entièrement par les 6 premières cases `C⁺` et ensuite plus que des `C⁻` jusqu'à la fin.
On pourrait craindre que cela affecte cette jolie structure de sommes se reportant de ligne en ligne pour conserver sa valeur égale à `F(399, 5)` : il n'en est rien. En effet, comme on le voit sur le schéma, le nœud `F(393, 0)` en bas à gauche du nœud `F(394, 0)` vient sauver la situation ! Nous venons de voir que ces deux valeurs étaient égales. En lui ajoutant donc les… 0 rivières issues de `C⁺·C⁺·C⁺·C⁺·C⁺·C⁺` dont la case suivante soit `C⁺`, on obtient le même schéma. On peut voir toujours la même égalité entre les deux nœuds cousin-cousine `F(393, 0)` : le `C⁺` issu de `F(394, 1)` et le `C⁻` issu de notre `F(394, 0)` qui ne donnera plus désormais que des `C⁻`.
Libre à vous en fait, on a aussi le droit de voir encore des divisions, mais dont le coefficient correspondant à `C⁺` serait désormais devenu nul. Le triangle de pascal a surtout un sens pour les `(n, k)` positifs avec `k ≤ n` mais après tout on pourrait décider arbitrairement de valeurs nulles hors de cette zone pour définir `C(n, k)` partout, et, vu notre définition de `F`, nous aurions pu écrire dans l'arbre quelque chose comme `F(393, -1)` dont la valeur serait nulle. Peut importe le jeu d'écriture, en tout cas on voit comment le jeu de report de ligne en ligne survit à la perturbation du bord. Regardez comme il se produit exactement la même chose dès qu'un nœud atteint `k = 0` (2 fois à la ligne suivante).
Vous me ferez sans doute grâce de faire un schéma similaire pour montrer ce qui se passe quand l'arrêt de la division est motivée par un manque et pas un excès de `C⁺`, j'ai déjà commis bien trop de schémas pour cet article. En tout cas je l'ai fait sur quantité de brouillons, et il se passe exactement la même chose en symétrique : sortie du triangle de Pascal, non plus pour cause de `k < 0` mais cette fois pour cause de `n < k` puisqu'on se retrouve à considérer des choses comme `F(6, 6)`, qui au lieu de se diviser en «`F(5, 6) + F(5, 5)`» à la ligne suivante donne simplement `F(5, 5)`, encore une fois égaux ensemble car égaux à `1/C(400,6)`. Exactement comme ci-dessus, on peut aussi très bien décréter qu'on a envie d'écrire quand même la division mais que `F(5, 6) = 0`. Peut importe, en tout cas ça marche. Faites-le, c'est hyper amusant. Allez, vous en mourrez d'envie.
## Résultat des courses
En tout cas, si on reprend notre formule (3) ci-dessus, on s'apperçoit grâce aux remarques que nous venons de faire ci-dessus qu'il aurait fallu écrire davantage de conditions de restrictions avec des minima. Regardons par exemple le facteur `F(399-q, 6-k)` dans la somme `Σ` de gauche correspondant au cas où la case en cours est `C⁻` : nous avons autorisé `k` à prendre toutes les valeurs dans `[0, min(q, 6)]`, mais si donc `q = 398` (on en est à tester la 398ème case) et `k = 0`, ce terme est en fait `F(1, 6)` ce qui… n'existe pas, à moins que nous ayons adopté la convention ci-dessus qu'hors du triangle de Pascal les `C(n,k)` soient nul, auquel cas ce terme devient nul lui-aussi et cesse de contribuer à la somme. Si nous regardons l'origine des `min` que nous avons déjà mis dans la formule, ils proviennent simplement du fait qu'il était plus évident que des valeurs trop grandes de `k` donneraient des valeurs négatives à `6-k` ou `5-k`, ce qui correspond au cas à la droite de l'arbre des cases `C⁺` trop vites consommés. Donc nous avons anticipé ce cas naturellement, mais notre analyse plus fine sur les schémas d'arbre a révélé l'autre cas un peu moins visible.
Finalement c'est peut-être plus simple de garder l'expression comme elle est et de seulement définir :
```
F(n, k) = C(n, k) / C(400, 6) si 0 ≤ k ≤ n
= 0 sinon
```
Et puis comme ça on n'a plus besoin de mettre des `min` sur les sommes et on peut tout rassembler pour réécrire (3) :
<pre>
(3) Pour n = q×p+r, P<sub>b</sub>(p, n) = 1 - ([Σ(k=0 → q) C(q, k)×[F(399-q, 6-k) + F(399-q, 5-k)×0.85<sup>r</sup>]×0.85<sup>k×p</sup>)
</pre>
Et si on faisait un petit rendu de cette belle formule ?
<div id="exact" class="graph"></div>
Plutôt joli, non ? Bon, déjà, la première bonne nouvelle c'est que ça a quand même une tête très voisine de ce qu'on avait, donc on n'a pas dit trop de bêtises la dernière fois en supposant une distribution uniforme de cases indépendantes pour simplifier.
Ensuite, on voit que les probabilités sont plutôt revues à la hausse, par exemple si on se place en `n = 400` ce qui correspond à une fouille complète de la rivière pour la stratégie `p = 1`. Surtout, en regardant attentivement cette valeur `Pb(1, 400) ≈ 0.6228505`, on s'apperçoit qu'on est maintenant sur la valeur théorique attendue. En effet, en faisant abstraction de toute modélisation des cases que ce soit, on sait qu'après 400 pêches à 1 pêche par case, on a fouillé toute la rivière exactement une fois. Donc la probabilité qu'on ait trouvé un Barpau à ce point est de `1 - 0.85⁶ ≈ 0.6228505`. Beaucoup, beaucoup plus satisfaisant que ce `0.5938` sorti d'on ne sait où que nous avions précédemment (enfin, si, on sait d'où, sorti d'un modèle où chaque case, indépendamment des autres, a `6/400` d'être `C⁺`).
Mais le plus surprenant dans ce nouveau graphique et qui montre bien que ces pseudo-exponentielles n'en sont pas, c'est qu'on les voit s'intersecter et se dépasser de temps à autre. Regardez ce qui arrive à `n = 800` ! Les stratégies `p = 1` et `p = 2` se rejoignent. C'était prévisible ! En 800 tentatives, à 1 pêche par case, on a eu le temps de (et je matérialise les façons de grouper les mots dans les phrases qui suivent parce que ça a du sens) «[tester toute la rivière] 2 fois», alors qu'en pêchant 2 fois par case, on a eu le temps de «[tester 2 fois] toute la rivière». Les deux sont bien évidemment équivalentes. La probabilité qu'on ait trouvé un Barpau en 800 cases est donc de `1 - 0.85^12` avec ces deux stratégies. Cette remarque se généralise : après `n = 400×p` pêches, la stratégie `p` rejoint la stratégie `1`.
Dernière remarque, allons voir ce qu'il en est à `n = 1200` pour confirmer la généralisation qui précède et voire la stratégie `p = 3` égaler temporairement la stratégie `p = 1`. Horreur ! Qu'apperçoit-on ? La stratégie `p = 3` a même dépassé la stratégie `p = 2` ! De loin, le graphique donnait pourtant l'impression de conserver la monotonie qu'avait la version simplifiée, et de dire que diminuer le facteur `p` était dans tous les cas une bonne idée. Et bien non ! Si vous avez pêché 1200 fois, à 3 pêches par cases vous avez la certitude d'avoir testé 18 fois une case à Barpau. Même remarque que ci-dessus, à 1 pêche par case aussi puisque vous avez fait 3 fois toute la rivière. Mais à `p = 2`… ?! Et bien non ! À 2 pêches par cases, vous n'avez couvert que 600 cases, c'est à dire que vous avez fouillé toute la rivière une fois (c'est bien, l'équivalent de 12 visites assurées sur une case à Barpau) mais… mais peut-être n'avez-vous pas trouvé 3 cases `C⁺` sur les 200 que vous avez parcourues dans votre deuxième «tour» de la rivière. Vous n'avez aucune garantie. Il existe un certains nombre de tirages de rivière pour lesquels vous n'avez même encore rencontré aucune case `C⁺` dans ce tour là. Et donc, temporairement, la stratégie `p = 3` est plus efficace que `p = 2` sur cette zone. Il y a en fait un effet de «résonnance» entre la taille de la rivière et le nombre de pêches tentées en tout. Dans tous les cas, la stratégie `p = 1`, qui «résonne» avec tout, reste la plus efficace et, seule, reste au-dessus de toutes les autres.
Je persiste donc : vous voulez avoir un Barpau vite ? Pêchez une fois par case, vraiment, même une analyse plus fine renforce ce résultat : c'est la stratégie optimale pour accélérer la rencontre de Barpaus.
<br>
[^P⁺P⁻]: vous avez reconnu `P⁺` et `P⁻` ? dans le précédent article, nous avions simplifé les fractions en `3/200` et `197/200`, mais ce sont bien les mêmes probabilités
<script src="/media/2020/Dans les arbres_graphs.js"></script>